In this post, we’ll dive into the core data structures at the heart of blockchain systems: the block chain and merkle tree. These fundamental structures play a crucial role in ensuring the integrity and functionality of many blockchain systems. Let’s delve into their significance and explore how they work together to enhance blockchain functionality.
Before we start, it’s essential to introduce a foundational concept that these data structures rely on: the hash pointer. A hash pointer serves as a reference to stored information coupled with a cryptographic hash of the data. Unlike a standard pointer that solely facilitates data retrieval, a hash pointer goes further by enabling data verification, ensuring its unaltered state. This concept provides the data structures with robust integrity characteristics, a quality we’ll delve into shortly.
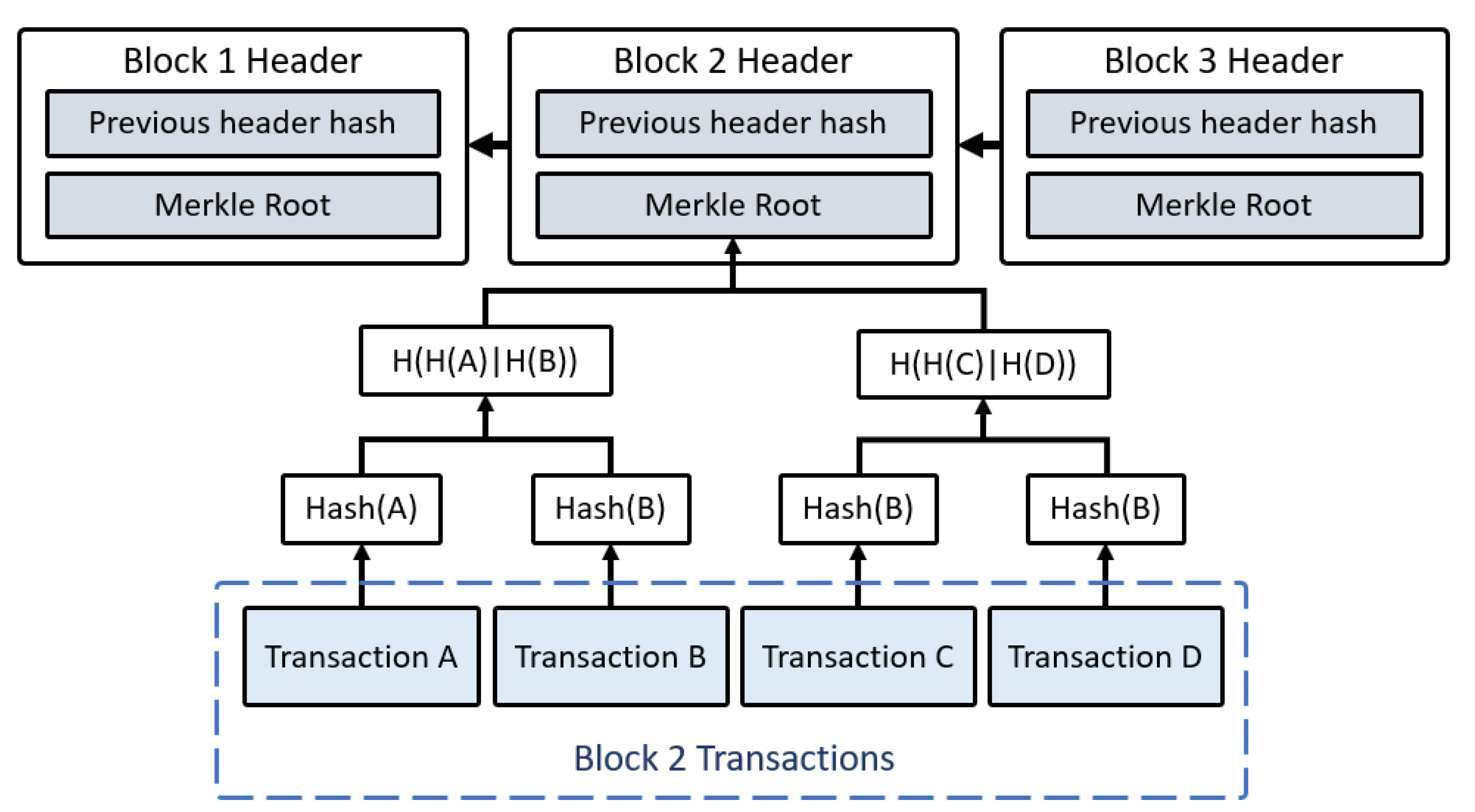
Let’s start off by taking a closer look at the block chain data structure. This structure is quite similar to something you might be familiar with - a linked list. The twist here is that instead of using regular pointers, the block chain uses hash pointers. So, each block not only keeps track of where the previous block’s value was located, but also includes a digest of that value. This digest lets us check if the value has been tampered with. At the top of this structure sits the head of the list, which is just a standard hash-pointer that points to the latest block.
A linked list is a linear data structure in which elements, called nodes, are connected sequentially through pointers or references. Each node contains two main parts: the data (or payload) it holds and a pointer (or reference) to the next node in the sequence.
Utilizing hash pointers, the structure of the block chain introduces a unique
integrity characteristic that prevents any manipulation of data in prior blocks;
it only permits the addition of new blocks to the sequence. To understand why a blockchain
achieves this characteristic, let’s consider what unfolds when a malicious entity
attempts to tamper with data within the middle of the chain. The adversary’s objective
is to carry out this tampering in a manner that those who retain only the hash
pointer at the chain’s outset remain oblivious to the tampering. To execute this,
the adversary alters the contents of a particular block, say block i. This alteration
results in a mismatch between the hash in block i + 1 and the modified block i,
since the hash in block i + 1 is computed over the entire contents of block i.
Notably, due to the collision-resistant nature of the hash function, we’re assured
that the new hash won’t align with the altered content. Consequently, the difference
between the revised data in block i and the hash pointer in block i + 1 is
detected. The adversary can attempt to conceal this alteration by adjusting the
hash of the subsequent block as well. This task can persist, yet it eventually
collapses upon reaching the chain’s starting point. As long as the hash pointer
at the chain’s origin is securely stored beyond the adversary’s reach, the ability
to modify any block without detection remains tricky to the adversary.
This aspect could offer an explanation for why the name “block chain” aptly describes the data structure, as opposed to terms like “secured linked-list” or similar variations. It is the chain-like behavior that tightly interlinks each block, preventing alterations during its lifespan due to its tamper-resistant nature. This robustness perfectly encapsulates the essence of the name “block chain.”
Now, let’s dive into the merkle tree data structure. This data structure is quite similar to something you might be familiar with again - a binary tree. In other words, a binary tree equipped with hash pointers goes by the name “merkle tree”. It was named after its inventor, Ralph Merkle. Ralph Merkle, along with his colleagues, introduced the concept of the merkle tree in the late 1970s.
In order to understand this data strutcure, imagine we have a set of data-containing blocks. These blocks serve as the tree’s leaves. We pair them up, and for each pair, we construct a unit with dual hash pointers, directed at the respective blocks. These units then form the next tier of the tree. Continuing this pattern, we group these units in pairs, crafting new structures containing hashes of each. This iterative process persists until we converge to a solitary block, which crowns the tree as its root. This merkle root is a crucial component of a merkle tree structure. It is the hash value that represents the entire set of data blocks within the merkle ree.
It is important to note that by retaining solely the hash pointer of the merkle root, we gain the ability to navigate down through the hash pointers to any location in the sequence. This allows us to validate data integrity, much like our observations with the block chain data structure. If an adversary alters a data block (leaf) lower in the tree, it disrupts the hash pointer one level above. Any continued tampering extends this change upward, eventually reaching the tree’s root where the tampering of the stored hash pointer becomes infeasible. Thus, any effort to manipulate data is readily detected by preserving the top hash pointer, the merkle root.
Another unique characteristic of merkle trees, in contrast to the block chain data structure, lies in their ability to provide concise membership proofs. Consider someone aiming to verify the membership of a specific data block within the merkle tree. We maintain the root as usual. They present the target data block, along with the blocks forming the path from the data block to the root. The remainder of the tree can be disregarded, as these path blocks suffice for verifying hashes up to the tree’s root. Thus, if after hashing from the data block (leaf) all the way up to the root matches with our stored root value, then we can proove that indeed that data block is part of the tree.
If the tree comprises of n nodes, approximately log(n) nodes must be presented.
With each step involving the computation of the child block’s hash, the verification
process typically takes around log(n) time. This is because you need to traverse
from the leaf to the root, verifying hashes at each level.
References
- Narayanan, A. et al. (2016) ‘Chapter 1: Introduction to Cryptography & Cryptocurrencies’, in Bitcoin and cryptocurrency technologies: A comprehensive introduction. Princeton, NJ: Princeton University Press.